3 Enumeration
Example: Bullying in Schools
To demonstrate mixture modeling in the training program and online resource components of the IES grant we utilize the Civil Rights Data Collection (CRDC)8 data repository. The CRDC is a federally mandated school-level data collection effort that occurs every other year. This public data is currently available for selected latent class indicators across 4 years (2011, 2013, 2015, 2017) and all US states. In this example, we use the Arizona state sample. We utilize six focal indicators which constitute the latent class model in our example; three variables which report on harassment/bullying in schools based on disability, race, or sex, and three variables on full-time equivalent school staff hires (counselor, psychologist, law enforcement). This data source also includes covariates on a variety of subjects and distal outcomes reported in 2018 such as math/reading assessments and graduation rates.
Load packages
library(tidyverse)
library(haven)
library(glue)
library(MplusAutomation)
library(here)
library(janitor)
library(gt)
library(cowplot)
library(DiagrammeR) 3.1 Variable Description
| LCA indicators1 | ||
| Name | Label | Values |
|---|---|---|
| leaid | District Identification Code | |
| ncessch | School Identification Code | |
| report_dis | Number of students harassed or bullied on the basis of disability | 0 = No reported incidents, 1 = At least one reported incident |
| report_race | Number of students harassed or bullied on the basis of race, color, or national origin | 0 = No reported incidents, 1 = At least one reported incident |
| report_sex | Number of students harassed or bullied on the basis of sex | 0 = No reported incidents, 1 = At least one reported incident |
| counselors_fte | Number of full time equivalent counselors hired as school staff | 0 = No staff present, 1 = At least one staff present |
| psych_fte | Number of full time equivalent psychologists hired as school staff | 0 = No staff present, 1 = At least one staff present |
| law_fte | Number of full time equivalent law enforcement officers hired as school staff | 0 = No staff present, 1 = At least one staff present |
| 1 Civil Rights Data Collection (CRDC) | ||
Variables have been transformed to be dichotomous indicators using the following coding strategy
Harassment and bullying count variables are recoded 1 if the school reported at least one incident of harassment (0 indicates no reported incidents).
On the original scale reported by the CDRC staff variables for full time equivalent employees (FTE) are represented as 1 and part time employees are represented by values between 1 and 0.
Schools with greater than one staff of the designated type are represented by values greater than 1.
All values greater than zero were recorded as 1s (e.g., .5, 1,3) indicating that the school has a staff present on campus at least part time.
Schools with no staff of the designated type are indicated as 0 for the dichotomous variable.
3.2 Prepare Data
df_bully <- read_csv(here("data", "crdc_lca_data.csv")) %>%
clean_names() %>%
dplyr::select(report_dis, report_race, report_sex, counselors_fte, psych_fte, law_fte) 3.3 Descriptive Statistics
# Set up data to find proportions of binary indicators
ds <- df_bully %>%
pivot_longer(c(report_dis, report_race, report_sex, counselors_fte, psych_fte, law_fte), names_to = "variable")
# Create table of variables and counts, then find proportions and round to 3 decimal places
prop_df <- ds %>%
count(variable, value) %>%
group_by(variable) %>%
mutate(prop = n / sum(n)) %>%
ungroup() %>%
mutate(prop = round(prop, 3))
# Make it a gt() table
prop_table <- prop_df %>%
gt(groupname_col = "variable", rowname_col = "value") %>%
tab_stubhead(label = md("*Values*")) %>%
tab_header(
md(
"Variable Proportions"
)
) %>%
cols_label(
variable = md("*Variable*"),
value = md("*Value*"),
n = md("*N*"),
prop = md("*Proportion*")
)
prop_table| Variable Proportions | ||
| Values | N | Proportion |
|---|---|---|
| counselors_fte | ||
| 0 | 1081 | 0.533 |
| 1 | 919 | 0.453 |
| NA | 27 | 0.013 |
| law_fte | ||
| 0 | 1749 | 0.863 |
| 1 | 251 | 0.124 |
| NA | 27 | 0.013 |
| psych_fte | ||
| 0 | 1050 | 0.518 |
| 1 | 947 | 0.467 |
| NA | 30 | 0.015 |
| report_dis | ||
| 0 | 1915 | 0.945 |
| 1 | 85 | 0.042 |
| NA | 27 | 0.013 |
| report_race | ||
| 0 | 1794 | 0.885 |
| 1 | 206 | 0.102 |
| NA | 27 | 0.013 |
| report_sex | ||
| 0 | 1660 | 0.819 |
| 1 | 340 | 0.168 |
| NA | 27 | 0.013 |
Save as image
3.4 Enumeration
This code uses the mplusObject function in the MplusAutomation package and saves all model runs in the enum folder.
lca_6 <- lapply(1:6, function(k) {
lca_enum <- mplusObject(
TITLE = glue("{k}-Class"),
VARIABLE = glue(
"categorical = report_dis-law_fte;
usevar = report_dis-law_fte;
classes = c({k}); "),
ANALYSIS =
"estimator = mlr;
type = mixture;
starts = 200 100;
processors = 10;",
OUTPUT = "sampstat residual tech11 tech14;",
PLOT =
"type = plot3;
series = report_dis-law_fte(*);",
usevariables = colnames(df_bully),
rdata = df_bully)
lca_enum_fit <- mplusModeler(lca_enum,
dataout=glue(here("enum", "bully.dat")),
modelout=glue(here("enum", "c{k}_bully.inp")) ,
check=TRUE, run = TRUE, hashfilename = FALSE)
})IMPORTANT: Before moving forward, make sure to open each output document to ensure models were estimated normally.
3.5 Examine and extract Mplus files
Code by Delwin Carter (2025)
Check all Models for:
- Warnings
- Errors
- Convergence and Loglikelihood Replication Information
source(here("functions", "extract_mplus_info.R"))
# Define the directory where all of the .out files are located.
output_dir <- here("enum")
# Get all .out files
output_files <- list.files(output_dir, pattern = "\\.out$", full.names = TRUE)
# Process all .out files into one dataframe
final_data <- map_dfr(output_files, extract_mplus_info_extended)
# Extract Sample_Size from final_data
sample_size <- unique(final_data$Sample_Size)3.5.1 Examine Mplus Warnings
source(here("functions", "extract_warnings.R"))
warnings_table <- extract_warnings(final_data)
warnings_table| Model Warnings | ||
| Output File | # of Warnings | Warning Message(s) |
|---|---|---|
| c1_bully.out | There are 5 warnings in the output file. | *** WARNING in VARIABLE command Note that only the first 8 characters of variable names are used in the output. Shorten variable names to avoid any confusion. |
*** WARNING in PLOT command Note that only the first 8 characters of variable names are used in plots. If variable names are not unique within the first 8 characters, problems may occur. |
||
*** WARNING in OUTPUT command SAMPSTAT option is not available when all outcomes are censored, ordered categorical, unordered categorical (nominal), count or continuous-time survival variables. Request for SAMPSTAT is ignored. |
||
*** WARNING in OUTPUT command TECH11 option is not available for TYPE=MIXTURE with only one class. Request for TECH11 is ignored. |
||
*** WARNING in OUTPUT command TECH14 option is not available for TYPE=MIXTURE with only one class. Request for TECH14 is ignored. |
||
| c2_bully.out | There are 3 warnings in the output file. | *** WARNING in VARIABLE command Note that only the first 8 characters of variable names are used in the output. Shorten variable names to avoid any confusion. |
*** WARNING in PLOT command Note that only the first 8 characters of variable names are used in plots. If variable names are not unique within the first 8 characters, problems may occur. |
||
*** WARNING in OUTPUT command SAMPSTAT option is not available when all outcomes are censored, ordered categorical, unordered categorical (nominal), count or continuous-time survival variables. Request for SAMPSTAT is ignored. |
||
| c3_bully.out | There are 3 warnings in the output file. | *** WARNING in VARIABLE command Note that only the first 8 characters of variable names are used in the output. Shorten variable names to avoid any confusion. |
*** WARNING in PLOT command Note that only the first 8 characters of variable names are used in plots. If variable names are not unique within the first 8 characters, problems may occur. |
||
*** WARNING in OUTPUT command SAMPSTAT option is not available when all outcomes are censored, ordered categorical, unordered categorical (nominal), count or continuous-time survival variables. Request for SAMPSTAT is ignored. |
||
| c4_bully.out | There are 3 warnings in the output file. | *** WARNING in VARIABLE command Note that only the first 8 characters of variable names are used in the output. Shorten variable names to avoid any confusion. |
*** WARNING in PLOT command Note that only the first 8 characters of variable names are used in plots. If variable names are not unique within the first 8 characters, problems may occur. |
||
*** WARNING in OUTPUT command SAMPSTAT option is not available when all outcomes are censored, ordered categorical, unordered categorical (nominal), count or continuous-time survival variables. Request for SAMPSTAT is ignored. |
||
| c5_bully.out | There are 3 warnings in the output file. | *** WARNING in VARIABLE command Note that only the first 8 characters of variable names are used in the output. Shorten variable names to avoid any confusion. |
*** WARNING in PLOT command Note that only the first 8 characters of variable names are used in plots. If variable names are not unique within the first 8 characters, problems may occur. |
||
*** WARNING in OUTPUT command SAMPSTAT option is not available when all outcomes are censored, ordered categorical, unordered categorical (nominal), count or continuous-time survival variables. Request for SAMPSTAT is ignored. |
||
| c6_bully.out | There are 3 warnings in the output file. | *** WARNING in VARIABLE command Note that only the first 8 characters of variable names are used in the output. Shorten variable names to avoid any confusion. |
*** WARNING in PLOT command Note that only the first 8 characters of variable names are used in plots. If variable names are not unique within the first 8 characters, problems may occur. |
||
*** WARNING in OUTPUT command SAMPSTAT option is not available when all outcomes are censored, ordered categorical, unordered categorical (nominal), count or continuous-time survival variables. Request for SAMPSTAT is ignored. |
||
# Save the warnings table
#gtsave(warnings_table, here("figures", "warnings_table.png"))3.5.2 Examine Mplus Errors
source(here("functions", "error_visualization.R"))
# Process errors
error_table_data <- process_error_data(final_data)
error_table_data| Model Estimation Errors | ||
| Output File | Model Type | Error Message |
|---|---|---|
| c2_bully.out | 2-Class | THE BEST LOGLIKELIHOOD VALUE HAS BEEN REPLICATED. RERUN WITH AT LEAST TWICE THE RANDOM STARTS TO CHECK THAT THE BEST LOGLIKELIHOOD IS STILL OBTAINED AND REPLICATED. |
| c3_bully.out | 3-Class | THE BEST LOGLIKELIHOOD VALUE HAS BEEN REPLICATED. RERUN WITH AT LEAST TWICE THE RANDOM STARTS TO CHECK THAT THE BEST LOGLIKELIHOOD IS STILL OBTAINED AND REPLICATED. IN THE OPTIMIZATION, ONE OR MORE LOGIT THRESHOLDS APPROACHED EXTREME VALUES OF -15.000 AND 15.000 AND WERE FIXED TO STABILIZE MODEL ESTIMATION. THESE VALUES IMPLY PROBABILITIES OF 0 AND 1. IN THE MODEL RESULTS SECTION, THESE PARAMETERS HAVE 0 STANDARD ERRORS AND 999 IN THE Z-SCORE AND P-VALUE COLUMNS. |
| c4_bully.out | 4-Class | THE BEST LOGLIKELIHOOD VALUE HAS BEEN REPLICATED. RERUN WITH AT LEAST TWICE THE RANDOM STARTS TO CHECK THAT THE BEST LOGLIKELIHOOD IS STILL OBTAINED AND REPLICATED. IN THE OPTIMIZATION, ONE OR MORE LOGIT THRESHOLDS APPROACHED EXTREME VALUES OF -15.000 AND 15.000 AND WERE FIXED TO STABILIZE MODEL ESTIMATION. THESE VALUES IMPLY PROBABILITIES OF 0 AND 1. IN THE MODEL RESULTS SECTION, THESE PARAMETERS HAVE 0 STANDARD ERRORS AND 999 IN THE Z-SCORE AND P-VALUE COLUMNS. |
| c5_bully.out | 5-Class | THE BEST LOGLIKELIHOOD VALUE HAS BEEN REPLICATED. RERUN WITH AT LEAST TWICE THE RANDOM STARTS TO CHECK THAT THE BEST LOGLIKELIHOOD IS STILL OBTAINED AND REPLICATED. IN THE OPTIMIZATION, ONE OR MORE LOGIT THRESHOLDS APPROACHED EXTREME VALUES OF -15.000 AND 15.000 AND WERE FIXED TO STABILIZE MODEL ESTIMATION. THESE VALUES IMPLY PROBABILITIES OF 0 AND 1. IN THE MODEL RESULTS SECTION, THESE PARAMETERS HAVE 0 STANDARD ERRORS AND 999 IN THE Z-SCORE AND P-VALUE COLUMNS. |
| c6_bully.out | 6-Class | THE BEST LOGLIKELIHOOD VALUE HAS BEEN REPLICATED. RERUN WITH AT LEAST TWICE THE RANDOM STARTS TO CHECK THAT THE BEST LOGLIKELIHOOD IS STILL OBTAINED AND REPLICATED. IN THE OPTIMIZATION, ONE OR MORE LOGIT THRESHOLDS APPROACHED EXTREME VALUES OF -15.000 AND 15.000 AND WERE FIXED TO STABILIZE MODEL ESTIMATION. THESE VALUES IMPLY PROBABILITIES OF 0 AND 1. IN THE MODEL RESULTS SECTION, THESE PARAMETERS HAVE 0 STANDARD ERRORS AND 999 IN THE Z-SCORE AND P-VALUE COLUMNS. |
# Save the errors table
#gtsave(error_table, here("figures", "error_table.png"))3.5.3 Examine Convergence and Loglikelihood Replications
source(here("functions", "summary_table.R"))
# Print Table with Superheader & Heatmap
summary_table <- create_flextable(final_data, sample_size)
summary_tableN = 2027 |
Random Starts |
Final starting value sets converging |
LL Replication |
Smallest Class |
||||||
|---|---|---|---|---|---|---|---|---|---|---|
Model |
Best LL |
npar |
Initial |
Final |
f |
% |
f |
% |
f |
% |
1-Class |
-5,443.409 |
6 |
200 |
100 |
100 |
100% |
100 |
100.0% |
2,027 |
100.0% |
2-Class |
-5,194.136 |
13 |
200 |
100 |
57 |
57% |
57 |
100.0% |
444 |
21.9% |
3-Class |
-5,122.478 |
20 |
200 |
100 |
93 |
93% |
80 |
86.0% |
216 |
10.6% |
4-Class |
-5,111.757 |
27 |
200 |
100 |
46 |
46% |
20 |
43.5% |
212 |
10.5% |
5-Class |
-5,105.589 |
34 |
200 |
100 |
37 |
37% |
7 |
18.9% |
43 |
2.1% |
6-Class |
-5,099.881 |
41 |
200 |
100 |
32 |
32% |
4 |
12.5% |
36 |
1.8% |
# Save the flextable as a PNG image
#invisible(save_as_image(summary_table, path = here("figures", "housekeeping.png")))3.5.4 Check for Loglikelihood Replication
Visualize and examine loglikelihood replication values for each ouput file individually
# Load the function for separate plots
source(here("functions", "ll_replication_plots.R"))
# Generate individual log-likelihood replication tables
ll_replication_tables <- generate_ll_replication_plots(final_data)
ll_replication_tables| Log Likelihood Replications: 1-Class | ||
| Source File: c1_bully.out | ||
| Log Likelihood | Replication Count | % of Valid Replications |
|---|---|---|
| −5,443.409 | 100.000 | 100.00% |
| Log Likelihood Replications: 2-Class | ||
| Source File: c2_bully.out | ||
| Log Likelihood | Replication Count | % of Valid Replications |
|---|---|---|
| −5,194.136 | 57.000 | 100.00% |
| Log Likelihood Replications: 3-Class | ||
| Source File: c3_bully.out | ||
| Log Likelihood | Replication Count | % of Valid Replications |
|---|---|---|
| −5,122.478 | 80.000 | 86.02% |
| −5,123.945 | 10.000 | 10.75% |
| −5,123.979 | 3.000 | 3.23% |
| Log Likelihood Replications: 4-Class | ||
| Source File: c4_bully.out | ||
| Log Likelihood | Replication Count | % of Valid Replications |
|---|---|---|
| −5,111.757 | 20.000 | 43.48% |
| −5,111.759 | 3.000 | 6.52% |
| −5,112.253 | 3.000 | 6.52% |
| −5,112.955 | 1.000 | 2.17% |
| −5,115.532 | 11.000 | 23.91% |
| −5,115.538 | 1.000 | 2.17% |
| −5,115.884 | 1.000 | 2.17% |
| −5,116.981 | 3.000 | 6.52% |
| −5,117.829 | 3.000 | 6.52% |
| Log Likelihood Replications: 5-Class | ||
| Source File: c5_bully.out | ||
| Log Likelihood | Replication Count | % of Valid Replications |
|---|---|---|
| −5,105.589 | 7.000 | 18.92% |
| −5,105.661 | 1.000 | 2.70% |
| −5,105.791 | 3.000 | 8.11% |
| −5,105.799 | 4.000 | 10.81% |
| −5,106.748 | 2.000 | 5.41% |
| −5,106.983 | 1.000 | 2.70% |
| −5,107.169 | 2.000 | 5.41% |
| −5,107.172 | 4.000 | 10.81% |
| −5,107.450 | 1.000 | 2.70% |
| −5,107.458 | 1.000 | 2.70% |
| −5,107.517 | 1.000 | 2.70% |
| −5,107.728 | 1.000 | 2.70% |
| −5,107.958 | 1.000 | 2.70% |
| −5,108.058 | 1.000 | 2.70% |
| −5,108.096 | 1.000 | 2.70% |
| −5,108.860 | 4.000 | 10.81% |
| −5,109.002 | 1.000 | 2.70% |
| −5,110.474 | 1.000 | 2.70% |
| Log Likelihood Replications: 6-Class | ||
| Source File: c6_bully.out | ||
| Log Likelihood | Replication Count | % of Valid Replications |
|---|---|---|
| −5,099.881 | 4.000 | 12.50% |
| −5,100.272 | 1.000 | 3.12% |
| −5,100.842 | 2.000 | 6.25% |
| −5,100.874 | 1.000 | 3.12% |
| −5,100.928 | 2.000 | 6.25% |
| −5,101.017 | 1.000 | 3.12% |
| −5,101.071 | 2.000 | 6.25% |
| −5,101.089 | 1.000 | 3.12% |
| −5,101.117 | 1.000 | 3.12% |
| −5,101.316 | 1.000 | 3.12% |
| −5,101.332 | 1.000 | 3.12% |
| −5,101.389 | 1.000 | 3.12% |
| −5,101.452 | 1.000 | 3.12% |
| −5,101.494 | 1.000 | 3.12% |
| −5,101.512 | 1.000 | 3.12% |
| −5,101.592 | 1.000 | 3.12% |
| −5,101.593 | 1.000 | 3.12% |
| −5,101.913 | 1.000 | 3.12% |
| −5,102.075 | 1.000 | 3.12% |
| −5,102.613 | 1.000 | 3.12% |
| −5,102.616 | 1.000 | 3.12% |
| −5,104.167 | 1.000 | 3.12% |
| −5,104.462 | 1.000 | 3.12% |
| −5,105.309 | 1.000 | 3.12% |
| −5,107.302 | 1.000 | 3.12% |
| −5,107.624 | 1.000 | 3.12% |
Visualize and examine loglikelihood replication for each output file together
ll_replication_table_all <- source(here("functions", "ll_replication_processing.R"), local = TRUE)$value
ll_replication_table_all1-Class |
2-Class |
3-Class |
4-Class |
5-Class |
6-Class |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
LL |
N |
% |
LL |
N |
% |
LL |
N |
% |
LL |
N |
% |
LL |
N |
% |
LL |
N |
% |
-5443.409 |
100 |
100 |
-5194.136 |
57 |
100 |
-5122.478 |
80 |
86 |
-5111.757 |
20 |
43.5 |
-5105.589 |
7 |
18.9 |
-5,099.881 |
4 |
12.5 |
— |
— |
— |
— |
— |
— |
-5123.945 |
10 |
10.8 |
-5111.759 |
3 |
6.5 |
-5105.661 |
1 |
2.7 |
-5,100.272 |
1 |
3.1 |
— |
— |
— |
— |
— |
— |
-5123.979 |
3 |
3.2 |
-5112.253 |
3 |
6.5 |
-5105.791 |
3 |
8.1 |
-5,100.842 |
2 |
6.2 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
-5112.955 |
1 |
2.2 |
-5105.799 |
4 |
10.8 |
-5,100.874 |
1 |
3.1 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
-5115.532 |
11 |
23.9 |
-5106.748 |
2 |
5.4 |
-5,100.928 |
2 |
6.2 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
-5115.538 |
1 |
2.2 |
-5106.983 |
1 |
2.7 |
-5,101.017 |
1 |
3.1 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
-5115.884 |
1 |
2.2 |
-5107.169 |
2 |
5.4 |
-5,101.071 |
2 |
6.2 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
-5116.981 |
3 |
6.5 |
-5107.172 |
4 |
10.8 |
-5,101.089 |
1 |
3.1 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
-5117.829 |
3 |
6.5 |
-5107.45 |
1 |
2.7 |
-5,101.117 |
1 |
3.1 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
-5107.458 |
1 |
2.7 |
-5,101.316 |
1 |
3.1 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
-5107.517 |
1 |
2.7 |
-5,101.332 |
1 |
3.1 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
-5107.728 |
1 |
2.7 |
-5,101.389 |
1 |
3.1 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
-5107.958 |
1 |
2.7 |
-5,101.452 |
1 |
3.1 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
-5108.058 |
1 |
2.7 |
-5,101.494 |
1 |
3.1 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
-5108.096 |
1 |
2.7 |
-5,101.512 |
1 |
3.1 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
-5108.86 |
4 |
10.8 |
-5,101.592 |
1 |
3.1 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
-5109.002 |
1 |
2.7 |
-5,101.593 |
1 |
3.1 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
-5110.474 |
1 |
2.7 |
-5,101.913 |
1 |
3.1 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
-5,102.075 |
1 |
3.1 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
-5,102.613 |
1 |
3.1 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
-5,102.616 |
1 |
3.1 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
-5,104.167 |
1 |
3.1 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
-5,104.462 |
1 |
3.1 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
-5,105.309 |
1 |
3.1 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
-5,107.302 |
1 |
3.1 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
-5,107.624 |
1 |
3.1 |

3.6 Table of Fit
First, extract data:
output_enum <- readModels(here("enum"), filefilter = "bully", quiet = TRUE)
# Extract fit indices
enum_extract <- LatexSummaryTable(
output_enum,
keepCols = c(
"Title",
"Parameters",
"LL",
"BIC",
"aBIC",
"BLRT_PValue",
"T11_VLMR_PValue",
"Observations"
),
sortBy = "Title"
)
# Calculate additional fit indices
allFit <- enum_extract %>%
mutate(CAIC = -2 * LL + Parameters * (log(Observations) + 1)) %>%
mutate(AWE = -2 * LL + 2 * Parameters * (log(Observations) + 1.5)) %>%
mutate(SIC = -.5 * BIC) %>%
mutate(expSIC = exp(SIC - max(SIC))) %>%
mutate(BF = exp(SIC - lead(SIC))) %>%
mutate(cmPk = expSIC / sum(expSIC)) %>%
dplyr::select(Title, Parameters, LL, BIC, aBIC, CAIC, AWE, BLRT_PValue, T11_VLMR_PValue, BF, cmPk) %>%
arrange(Parameters)
# Merge columns with LL replications and class size from `final_data`
merged_table <- allFit %>%
mutate(Title = str_trim(Title)) %>%
left_join(
final_data %>%
select(
Class_Model,
Perc_Convergence,
Replicated_LL_Perc,
Smallest_Class,
Smallest_Class_Perc
),
by = c("Title" = "Class_Model")
) %>%
mutate(Smallest_Class = coalesce(Smallest_Class, final_data$Smallest_Class[match(Title, final_data$Class_Model)])) %>%
relocate(Perc_Convergence, Replicated_LL_Perc, .after = LL) %>%
mutate(Smallest_Class_Combined = paste0(Smallest_Class, "\u00A0(", Smallest_Class_Perc, "%)")) %>%
select(
Title,
Parameters,
LL,
Perc_Convergence,
Replicated_LL_Perc,
BIC,
aBIC,
CAIC,
AWE,
T11_VLMR_PValue,
BLRT_PValue,
Smallest_Class_Combined,
BF,
cmPk
)Then, create table:
fit_table1 <- merged_table %>%
select(Title, Parameters, LL, Perc_Convergence, Replicated_LL_Perc,
BIC, aBIC, CAIC, AWE,
T11_VLMR_PValue, BLRT_PValue,
Smallest_Class_Combined) %>%
gt() %>%
tab_header(title = md("**Model Fit Summary Table**")) %>%
tab_spanner(label = "Model Fit Indices", columns = c(BIC, aBIC, CAIC, AWE)) %>%
tab_spanner(label = "LRTs", columns = c(T11_VLMR_PValue, BLRT_PValue)) %>%
tab_spanner(label = md("Smallest\u00A0Class"), columns = c(Smallest_Class_Combined)) %>%
cols_label(
Title = "Classes",
Parameters = md("Par"),
LL = md("*LL*"),
Perc_Convergence = "% Converged",
Replicated_LL_Perc = "% Replicated",
BIC = "BIC",
aBIC = "aBIC",
CAIC = "CAIC",
AWE = "AWE",
T11_VLMR_PValue = "VLMR",
BLRT_PValue = "BLRT",
Smallest_Class_Combined = "n (%)"
) %>%
tab_footnote(
footnote = md(
"*Note.* Par = Parameters; *LL* = model log likelihood;
BIC = Bayesian information criterion;
aBIC = sample size adjusted BIC; CAIC = consistent Akaike information criterion;
AWE = approximate weight of evidence criterion;
BLRT = bootstrapped likelihood ratio test p-value;
VLMR = Vuong-Lo-Mendell-Rubin adjusted likelihood ratio test p-value;
*cmPk* = approximate correct model probability."
),
locations = cells_title()
) %>%
tab_options(column_labels.font.weight = "bold") %>%
fmt_number(
columns = c(3, 6:9),
decimals = 2
) %>%
sub_missing(1:11,
missing_text = "--") %>%
fmt(
c(T11_VLMR_PValue, BLRT_PValue),
fns = function(x)
ifelse(x < 0.001, "<.001",
scales::number(x, accuracy = .01))
) %>%
fmt_percent(
columns = c(Perc_Convergence, Replicated_LL_Perc),
decimals = 0,
scale_values = FALSE
) %>%
cols_align(align = "center", columns = everything()) %>%
tab_style(
style = list(cell_text(weight = "bold")),
locations = list(
cells_body(columns = BIC, row = BIC == min(BIC)),
cells_body(columns = aBIC, row = aBIC == min(aBIC)),
cells_body(columns = CAIC, row = CAIC == min(CAIC)),
cells_body(columns = AWE, row = AWE == min(AWE)),
cells_body(columns = T11_VLMR_PValue,
row = ifelse(T11_VLMR_PValue < .05 & lead(T11_VLMR_PValue) > .05, T11_VLMR_PValue < .05, NA)),
cells_body(columns = BLRT_PValue,
row = ifelse(BLRT_PValue < .05 & lead(BLRT_PValue) > .05, BLRT_PValue < .05, NA))
)
)
fit_table1| Model Fit Summary Table1 | |||||||||||
| Classes | Par | LL | % Converged | % Replicated |
Model Fit Indices
|
LRTs
|
Smallest Class
|
||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| BIC | aBIC | CAIC | AWE | VLMR | BLRT | n (%) | |||||
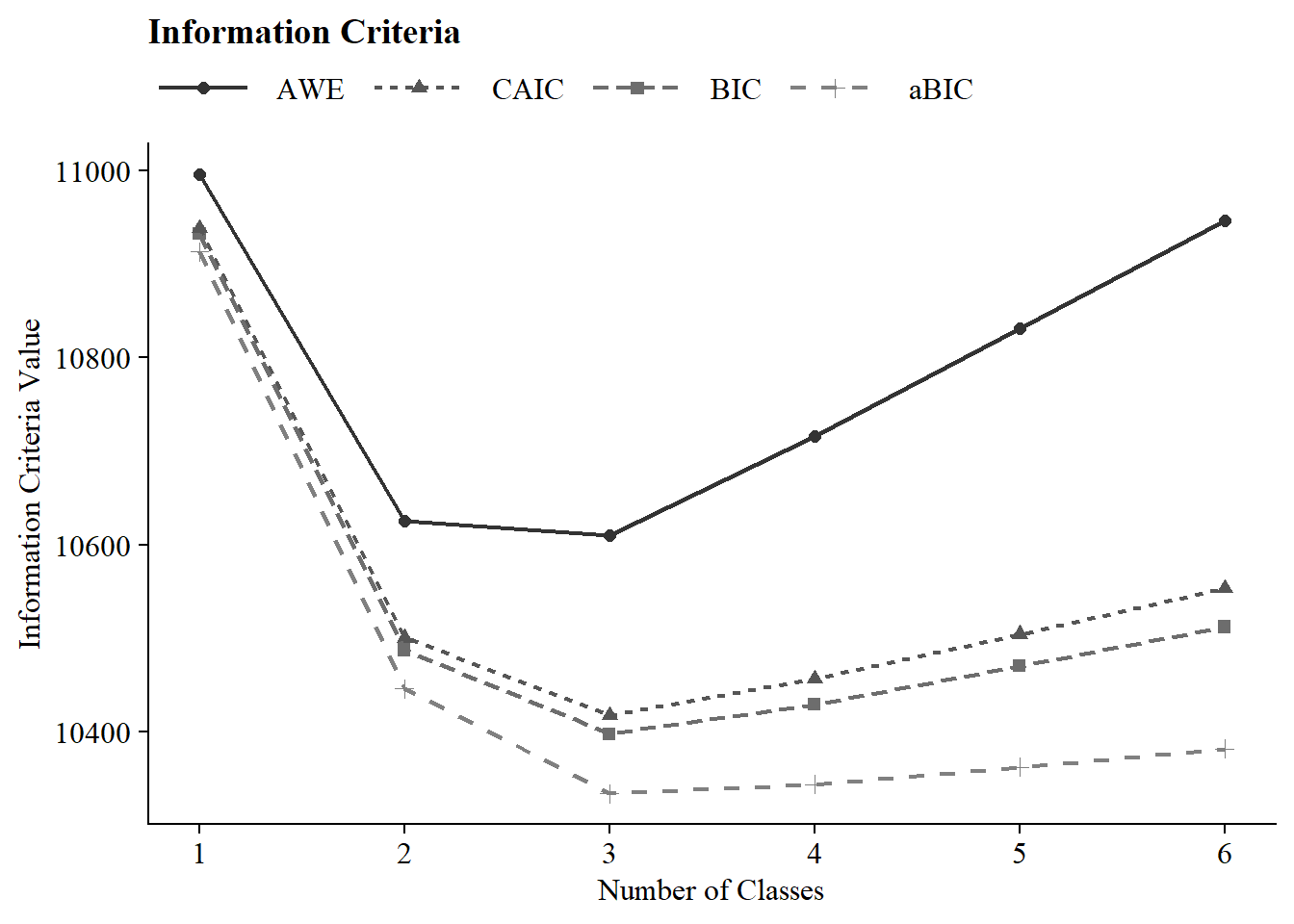
| 1-Class | 6 | −5,443.41 | 100% | 100% | 10,932.50 | 10,913.44 | 10,938.50 | 10,996.19 | – | – | 2027 (100%) |
| 2-Class | 13 | −5,194.14 | 57% | 100% | 10,487.26 | 10,445.96 | 10,500.26 | 10,625.24 | <.001 | <.001 | 444 (21.9%) |
| 3-Class | 20 | −5,122.48 | 93% | 86% | 10,397.24 | 10,333.70 | 10,417.24 | 10,609.53 | <.001 | <.001 | 216 (10.6%) |
| 4-Class | 27 | −5,111.76 | 46% | 44% | 10,429.10 | 10,343.32 | 10,456.10 | 10,715.69 | 0.01 | <.001 | 212 (10.5%) |
| 5-Class | 34 | −5,105.59 | 37% | 19% | 10,470.07 | 10,362.04 | 10,504.06 | 10,830.95 | 0.18 | 0.29 | 43 (2.1%) |
| 6-Class | 41 | −5,099.88 | 32% | 12% | 10,511.95 | 10,381.69 | 10,552.95 | 10,947.14 | 0.18 | 0.38 | 36 (1.8%) |
| 1 Note. Par = Parameters; LL = model log likelihood; BIC = Bayesian information criterion; aBIC = sample size adjusted BIC; CAIC = consistent Akaike information criterion; AWE = approximate weight of evidence criterion; BLRT = bootstrapped likelihood ratio test p-value; VLMR = Vuong-Lo-Mendell-Rubin adjusted likelihood ratio test p-value; cmPk = approximate correct model probability. | |||||||||||
Save table
3.7 Information Criteria Plot
allFit %>%
dplyr::select(2:7) %>%
rowid_to_column() %>%
pivot_longer(`BIC`:`AWE`,
names_to = "Index",
values_to = "ic_value") %>%
mutate(Index = factor(Index,
levels = c ("AWE", "CAIC", "BIC", "aBIC"))) %>%
ggplot(aes(
x = rowid,
y = ic_value,
color = Index,
shape = Index,
group = Index,
lty = Index
)) +
geom_point(size = 2.0) + geom_line(linewidth = .8) +
scale_x_continuous(breaks = 1:nrow(allFit)) +
scale_colour_grey(end = .5) +
theme_cowplot() +
labs(x = "Number of Classes", y = "Information Criteria Value", title = "Information Criteria") +
theme(
text = element_text(family = "serif", size = 12),
legend.text = element_text(family="serif", size=12),
legend.key.width = unit(3, "line"),
legend.title = element_blank(),
legend.position = "top"
)
Save figure
3.8 Compare Class Solutions
Compare probability plots for \(K = 1:6\) class solutions
model_results <- data.frame()
for (i in 1:length(output_enum)) {
temp <- output_enum[[i]]$parameters$probability.scale %>%
mutate(model = paste(i,"-Class Model"))
model_results <- rbind(model_results, temp)
}
rm(temp)
compare_plot <-
model_results %>%
filter(category == 2) %>%
dplyr::select(est, model, LatentClass, param) %>%
mutate(param = as.factor(str_to_lower(param)))
compare_plot$param <- fct_inorder(compare_plot$param)
ggplot(
compare_plot,
aes(
x = param,
y = est,
color = LatentClass,
shape = LatentClass,
group = LatentClass,
lty = LatentClass
)
) +
geom_point() +
geom_line() +
scale_colour_viridis_d() +
facet_wrap( ~ model, ncol = 2) +
labs(title = "Bullying Items",
x = " ", y = "Probability") +
theme_minimal() +
theme(panel.grid.major.y = element_blank(),
axis.text.x = element_text(angle = -45, hjust = -.1)) 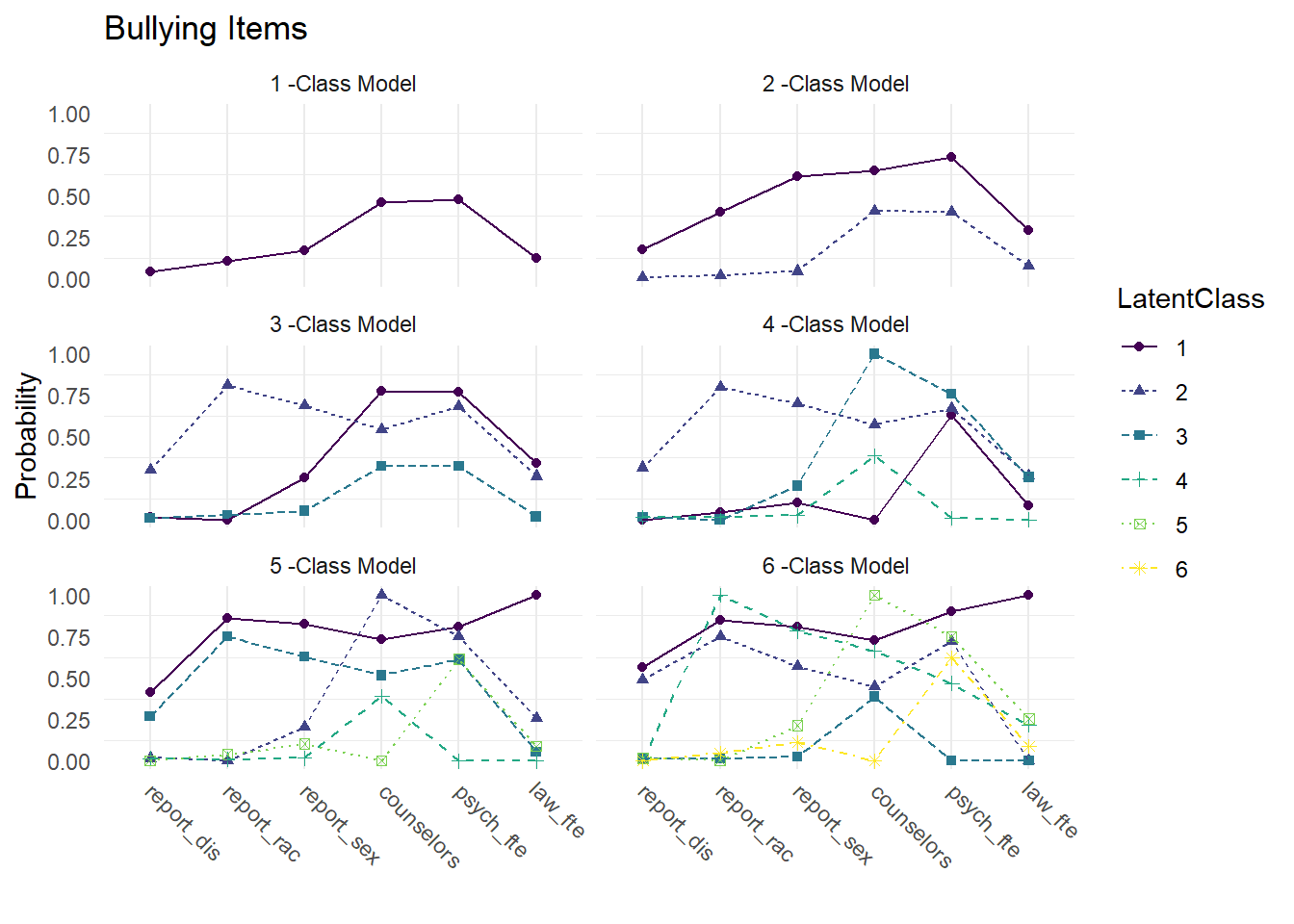
Save figure:
3.9 3-Class Probability Plot
Use the plot_lca function provided in the folder to plot the item probability plot. This function requires one argument:
- model_name: The name of the Mplus readModels object (e.g., output_enum$c3_bully.out)
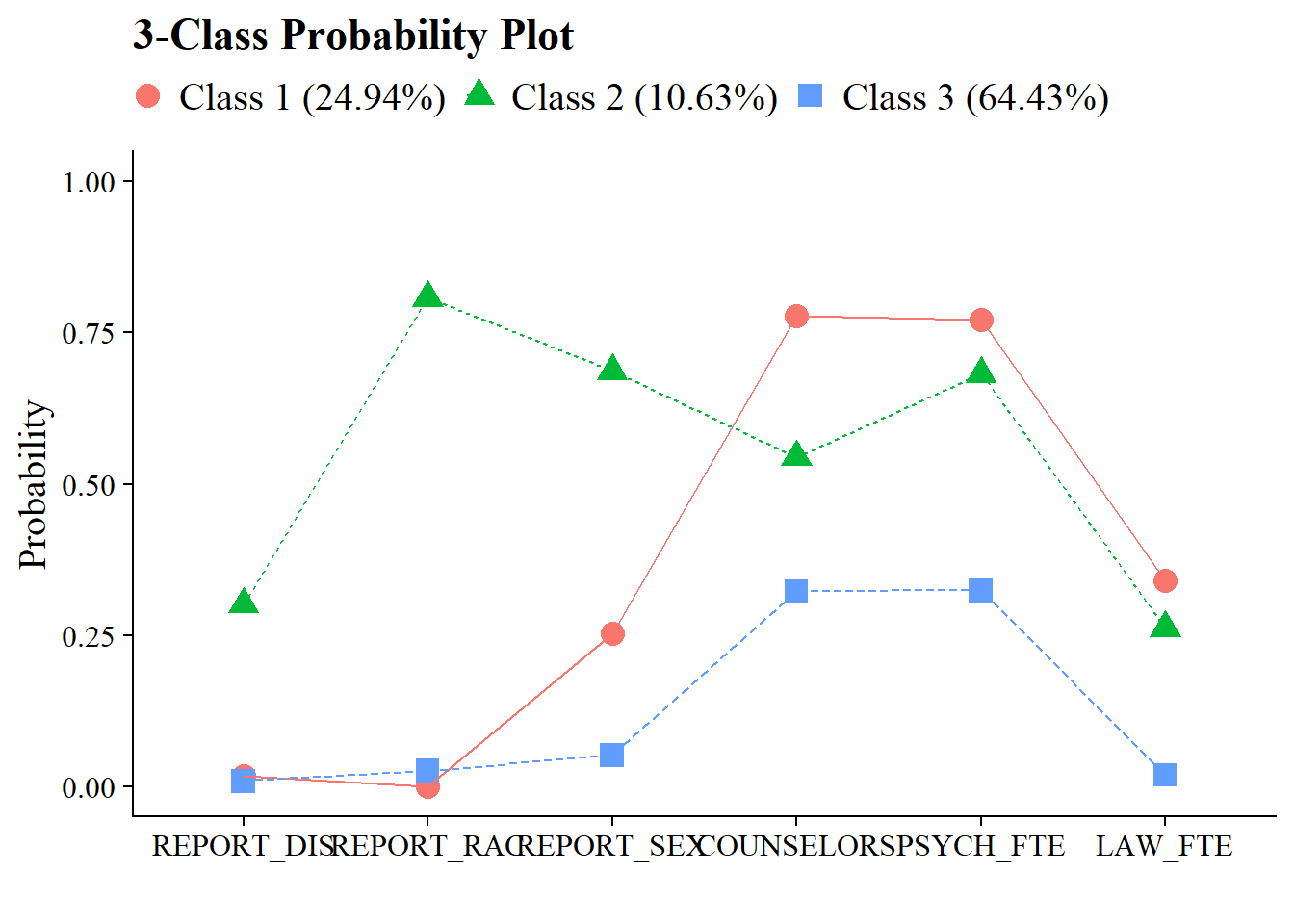
Save figure:
3.10 Observed Response Patterns
Save response frequencies for the 3-class model from the previous lab with response is _____.dat under SAVEDATA.
patterns <- mplusObject(
TITLE = "C3 LCA - Save response patterns",
VARIABLE =
"categorical = report_dis-law_fte;
usevar = report_dis-law_fte;
classes = c(3);",
ANALYSIS =
"estimator = mlr;
type = mixture;
starts = 0;
processors = 10;
optseed = 802779;",
SAVEDATA =
"File=savedata.dat;
Save=cprob;
! Code to save response frequency data
response is resp_patterns.dat;",
OUTPUT = "residual patterns tech11 tech14",
usevariables = colnames(df_bully),
rdata = df_bully)
patterns_fit <- mplusModeler(patterns,
dataout=here("mplus", "bully.dat"),
modelout=here("mplus", "patterns.inp") ,
check=TRUE, run = TRUE, hashfilename = FALSE)Read in observed response pattern data and relabel the columns
# Read in response frequency data that we just created:
patterns <- read_table(here("mplus", "resp_patterns.dat"),
col_names=FALSE, na = "*")
# Extract the column names
names <- names(readModels(here("mplus", "patterns.out"))[['savedata']])
# Add the names back to the dataset
colnames(patterns) <- c("Frequency", names) Create a table with the top 5 unconditional response pattern, then top of conditional response pattern for each modal class assignment
# Order responses by highest frequency
order_highest <- patterns %>%
arrange(desc(Frequency))
# Loop `patterns` data to list top 5 conditional response patterns for each class
loop_cond <- lapply(1:max(patterns$C), function(k) {
order_cond <- patterns %>%
filter(C == k) %>%
arrange(desc(Frequency)) %>%
head(5)
})
# Convert loop into data frame
table_data <- as.data.frame(bind_rows(loop_cond))
# Combine unconditional and conditional responses patterns
response_patterns <- rbind(order_highest[1:5,], table_data) Finally, use gt to make a nicely formatted table
resp_table <- response_patterns %>%
gt() %>%
tab_header(
title = "Observed Response Patterns",
subtitle = html("Response patterns, estimated frequencies, estimated posterior class probabilities and modal assignments")) %>%
tab_source_note(
source_note = md("Data Source: **Civil Rights Data Collection (CRDC)**")) %>%
cols_label(
Frequency = html("<i>f</i><sub>r</sub>"),
REPORT_D = "Harrassment: Disability",
REPORT_R = "Harrassment: Race",
REPORT_S = "Harrassment: Sex",
COUNSELO = "Staff: Counselor",
PSYCH_FT = "Staff: Psychologist",
LAW_FTE = "Staff: Law Enforcement",
CPROB1 = html("P<sub><i>k</i></sub>=1"),
CPROB2 = html("P<sub><i>k</i></sub>=2"),
CPROB3 = html("P<sub><i>k</i></sub>=3"),
C = md("*k*")) %>%
tab_row_group(
label = "Unconditional response patterns",
rows = 1:5) %>%
tab_row_group(
label = md("*k* = 1 Conditional response patterns"),
rows = 6:10) %>% #EDIT THESE VALUES BASED ON THE LAST COLUMN
tab_row_group(
label = md("*k* = 2 Conditional response patterns"),
rows = 11:15) %>% #EDIT THESE VALUES BASED ON THE LAST COLUMN
tab_row_group(
label = md("*k* = 3 Conditional response patterns"),
rows = 16:20) %>% #EDIT THESE VALUES BASED ON THE LAST COLUMN
row_group_order(
groups = c("Unconditional response patterns",
md("*k* = 1 Conditional response patterns"),
md("*k* = 2 Conditional response patterns"),
md("*k* = 3 Conditional response patterns"))) %>%
tab_footnote(
footnote = html(
"<i>Note.</i> <i>f</i><sub>r</sub> = response pattern frequency; P<sub><i>k</i></sub> = posterior class probabilities"
)
) %>%
cols_align(align = "center") %>%
opt_align_table_header(align = "left") %>%
gt::tab_options(table.font.names = "Times New Roman")
resp_table| Observed Response Patterns | ||||||||||
| Response patterns, estimated frequencies, estimated posterior class probabilities and modal assignments | ||||||||||
| fr | Harrassment: Disability | Harrassment: Race | Harrassment: Sex | Staff: Counselor | Staff: Psychologist | Staff: Law Enforcement | Pk=1 | Pk=2 | Pk=3 | k |
|---|---|---|---|---|---|---|---|---|---|---|
| Unconditional response patterns | ||||||||||
| 525 | 0 | 0 | 0 | 0 | 0 | 0 | 0.023 | 0.002 | 0.976 | 3 |
| 299 | 0 | 0 | 0 | 0 | 1 | 0 | 0.139 | 0.007 | 0.854 | 3 |
| 293 | 0 | 0 | 0 | 1 | 0 | 0 | 0.146 | 0.004 | 0.850 | 3 |
| 251 | 0 | 0 | 0 | 1 | 1 | 0 | 0.541 | 0.009 | 0.449 | 1 |
| 75 | 0 | 0 | 0 | 1 | 1 | 1 | 0.959 | 0.011 | 0.030 | 1 |
| k = 1 Conditional response patterns | ||||||||||
| 251 | 0 | 0 | 0 | 1 | 1 | 0 | 0.541 | 0.009 | 0.449 | 1 |
| 75 | 0 | 0 | 0 | 1 | 1 | 1 | 0.959 | 0.011 | 0.030 | 1 |
| 72 | 0 | 0 | 1 | 1 | 1 | 0 | 0.803 | 0.088 | 0.108 | 1 |
| 38 | 0 | 0 | 1 | 0 | 1 | 0 | 0.431 | 0.139 | 0.430 | 1 |
| 34 | 0 | 0 | 0 | 0 | 1 | 1 | 0.789 | 0.027 | 0.184 | 1 |
| k = 2 Conditional response patterns | ||||||||||
| 24 | 0 | 1 | 0 | 0 | 1 | 0 | 0.000 | 0.561 | 0.439 | 2 |
| 20 | 0 | 1 | 1 | 0 | 1 | 0 | 0.000 | 0.981 | 0.019 | 2 |
| 19 | 0 | 1 | 1 | 1 | 1 | 0 | 0.000 | 0.992 | 0.008 | 2 |
| 18 | 0 | 1 | 1 | 1 | 0 | 0 | 0.000 | 0.967 | 0.033 | 2 |
| 12 | 0 | 1 | 1 | 1 | 1 | 1 | 0.000 | 1.000 | 0.000 | 2 |
| k = 3 Conditional response patterns | ||||||||||
| 525 | 0 | 0 | 0 | 0 | 0 | 0 | 0.023 | 0.002 | 0.976 | 3 |
| 299 | 0 | 0 | 0 | 0 | 1 | 0 | 0.139 | 0.007 | 0.854 | 3 |
| 293 | 0 | 0 | 0 | 1 | 0 | 0 | 0.146 | 0.004 | 0.850 | 3 |
| 36 | 0 | 0 | 1 | 0 | 0 | 0 | 0.117 | 0.060 | 0.823 | 3 |
| 27 | 0 | 0 | 0 | NA | NA | NA | 0.236 | 0.006 | 0.758 | 3 |
| Data Source: Civil Rights Data Collection (CRDC) | ||||||||||
| Note. fr = response pattern frequency; Pk = posterior class probabilities | ||||||||||
Save table:
3.11 Classification Diagnostics
Use Mplus to calculate k-class confidence intervals (Note: Change the synax to make your chosen k-class model):
classification <- mplusObject(
TITLE = "C3 LCA - Calculated k-Class 95% CI",
VARIABLE =
"categorical = report_dis-law_fte;
usevar = report_dis-law_fte;
classes = c(3);",
ANALYSIS =
"estimator = ml;
type = mixture;
starts = 0;
processors = 10;
optseed = 802779;
bootstrap = 1000;",
MODEL =
"
!CHANGE THIS SECTION TO YOUR CHOSEN k-CLASS MODEL
%OVERALL%
[C#1](c1);
[C#2](C2);
Model Constraint:
New(p1 p2 p3);
p1 = exp(c1)/(1+exp(c1)+exp(c2));
p2 = exp(c2)/(1+exp(c1)+exp(c2));
p3 = 1/(1+exp(c1)+exp(c2));",
OUTPUT = "cinterval(bcbootstrap)",
usevariables = colnames(df_bully),
rdata = df_bully)
classification_fit <- mplusModeler(classification,
dataout=here("mplus", "bully.dat"),
modelout=here("mplus", "class.inp") ,
check=TRUE, run = TRUE, hashfilename = FALSE)Note: Ensure that the classes did not shift during this step (i.g., Class 1 in the enumeration run is now Class 4). Evaluate output and compare the class counts and proportions for the latent classes. Using the OPTSEED function ensures replication of the best loglikelihood value run.
Read in the 3-class model:
# Read in the 3-class model and extract information needed
output_enum <- readModels(here("mplus", "class.out"))
# Entropy
entropy <- c(output_enum$summaries$Entropy, rep(NA, output_enum$summaries$NLatentClasses-1))
# 95% k-Class and k-class 95% Confidence Intervals
k_ci <- output_enum$parameters$ci.unstandardized %>%
filter(paramHeader == "New.Additional.Parameters") %>%
unite(CI, c(low2.5,up2.5), sep=", ", remove = TRUE) %>%
mutate(CI = paste0("[", CI, "]")) %>%
rename(kclass=est) %>%
dplyr::select(kclass, CI)
# AvePPk = Average Latent Class Probabilities for Most Likely Latent Class Membership (Row) by Latent Class (Column)
avePPk <- tibble(avePPk = diag(output_enum$class_counts$avgProbs.mostLikely))
# mcaPk = modal class assignment proportion
mcaPk <- round(output_enum$class_counts$mostLikely,3) %>%
mutate(model = paste0("Class ", class)) %>%
add_column(avePPk, k_ci) %>%
rename(mcaPk = proportion) %>%
dplyr::select(model, kclass, CI, mcaPk, avePPk)
# OCCk = odds of correct classification
OCCk <- mcaPk %>%
mutate(OCCk = round((avePPk/(1-avePPk))/(kclass/(1-kclass)),3))
# Put everything together
class_table <- data.frame(OCCk, entropy)Now, use gt to make a nicely formatted table
class_table <- class_table %>%
gt() %>%
tab_header(
title = "Model Classification Diagnostics for the 3-Class Solution") %>%
cols_label(
model = md("*k*-Class"),
kclass = md("*k*-Class Proportions"),
CI = "95% CI",
mcaPk = html("McaP<sub>k</sub>"),
avePPk = md("AvePP<sub>k</sub>"),
OCCk = md("OCC<sub>k</sub>"),
entropy = "Entropy") %>%
sub_missing(7,
missing_text = "") %>%
tab_footnote(
footnote = html(
"<i>Note.</i> McaP<sub>k</sub> = Modal class assignment proportion; AvePP<sub>k</sub> = Average posterior class probabilities; OCC<sub>k</sub> = Odds of correct classification; "
)
) %>%
cols_align(align = "center") %>%
opt_align_table_header(align = "left") %>%
gt::tab_options(table.font.names = "Times New Roman")
class_table| Model Classification Diagnostics for the 3-Class Solution | ||||||
| k-Class | k-Class Proportions | 95% CI | McaPk | AvePPk | OCCk | Entropy |
|---|---|---|---|---|---|---|
| Class 1 | 0.249 | [0.166, 0.329] | 0.282 | 0.675 | 6.264 | 0.635 |
| Class 2 | 0.106 | [0.083, 0.136] | 0.095 | 0.904 | 79.420 | |
| Class 3 | 0.644 | [0.561, 0.731] | 0.623 | 0.893 | 4.614 | |
| Note. McaPk = Modal class assignment proportion; AvePPk = Average posterior class probabilities; OCCk = Odds of correct classification; | ||||||
